Rotations in Three-Dimensions:
Euler Angles and Rotation Matrices
Part 2 – Summary and Sample Code
D. Rose - February, 2015
Abstract
This paper describes a commonly used set of Tait-Bryan Euler angles, shows how to convert from Euler angles to a rotation matrix and back, how to rotate objects in both the forward and reverse direction, and how to concatenate multiple rotations into a single rotation matrix.
The paper is divided into two parts. Part 1 provides a detailed explanation of the relevant assumptions, conventions and math. Part 2 provides a summary of the key equations, along with sample code in Java. (See the links at the top of the page.)
Euler Angle Conventions
The following conventions are used in this paper. For a detailed explanation of what they mean—and what the alternatives are—see Part 1.
- Tait-Bryan variant of Euler Angles
- Yaw-pitch-roll rotation order, rotating around the z, y and x axes respectively
- Intrinsic rotation
- Active (otherwise known as alibi) rotation
- Right-handed coordinate system with right-handed rotations
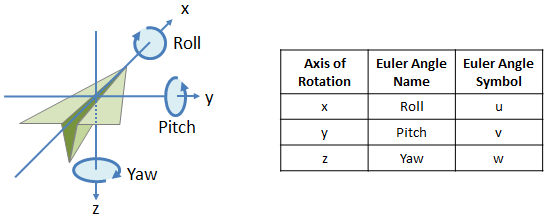
Figure 1: Euler Angle Axes, Names and Symbol Convention
Rotation order is: (1) Yaw, (2) Pitch and (3) Roll
Rotation Matrices
A rotation matrix is composed of nine numbers arranged in a 3x3 matrix like this:

(eq 1)
Code sample 1 shows a minimal data structure for representing a 3x3 rotation matrix. This object will be used throughout the subsequent code examples.
Code Sample 1: Rotation Matrix Data Structure
public class RotationMatrix
{
public double r11 = 0; //First row
public double r12 = 0;
public double r13 = 0;
public double r21 = 0; //Second row
public double r22 = 0;
public double r23 = 0;
public double r31 = 0; //Third row
public double r32 = 0;
public double r33 = 0;
}
Converting Euler Angles to a Rotation Matrix
A rotation matrix can be derived from the three Euler angles as shown in Equation 2:
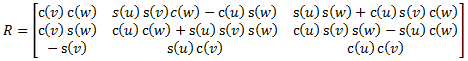
(eq 2)
where:
| (u, v, w) are the three Euler angles (roll, pitch, yaw), corresponding to rotations around the x, y and z axes | |
| c() and s() are shorthand for cosine and sine |
The corresponding Java method is shown in Code Sample 2. The inputs are the three Euler angles (in radians) in the order yaw, pitch and roll. The method first computes all the necessary sine and cosine values, creates an empty rotation matrix object, then populates the matrix as defined in equation 2. It returns the fully-populated rotation matrix object.
Code Sample 2: Creating a Rotation Matrix from Euler Angles
public static RotationMatrix yawPitchRollToMatrix(
double yaw, //Yaw angle (radians)
double pitch, //Pitch angle (radians)
double roll ) //Roll angle (radians)
{
//Precompute sines and cosines of Euler angles
double su = Math.sin(roll);
double cu = Math.cos(roll);
double sv = Math.sin(pitch);
double cv = Math.cos(pitch);
double sw = Math.sin(yaw);
double cw = Math.cos(yaw);
//Create and populate RotationMatrix
RotationMatrix A = new RotationMatrix();
A.r11 = cv*cw;
A.r12 = su*sv*cw - cu*sw;
A.r13 = su*sw + cu*sv*cw;
A.r21 = cv*sw;
A.r22 = cu*cw + su*sv*sw;
A.r23 = cu*sv*sw - su*cw;
A.r31 = -sv;
A.r32 = su*cv;
A.r33 = cu*cv;
return A;
}
Converting a Rotation Matrix to Euler Angles
The general solution for recovering Euler angles from a rotation matrix is:
| Yaw angle: | 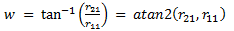 |
(eq 3a) |
|
| Pitch angle: | 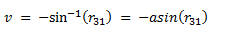 |
(eq 3b) |
|
| Roll angle: |  |
(eq 3c) |
If pitch angle v = −90°, then r31 will equal 1, and;
If pitch angle v = +90°, then r31 will equal −1, and;
In practice, it is usual to set one of the angles (u) or (w) to zero and solve for the other.
Code Sample 3 implements this solution, including the special case handling. The input is a populated rotation matrix, and the return value is a three element array containing the yaw, pitch and roll angles (in that order) in radians. Note that if the code detects the gimbal lock condition, it sets the yaw angle (w) to zero, and solves for the roll angle (u).
This code will return values of roll and yaw between −π and +π radians, and pitch angles between −π/2 and +π/2 radians.
Code Sample 3: Extracting Euler Angles from a Rotation Matrix
public static double[] MatrixToYawPitchRoll( RotationMatrix A )
{
double[] angle = new double[3];
angle[1] = -Math.asin( A.r31 ); //Pitch
//Gymbal lock: pitch = -90
if( A.r31 == 1 ){
angle[0] = 0.0; //yaw = 0
angle[2] = Math.atan2( -A.r12, -A.r13 ); //Roll
System.out.println("Gimbal lock: pitch = -90");
}
//Gymbal lock: pitch = 90
else if( A.r31 == -1 ){
angle[0] = 0.0; //yaw = 0
angle[2] = Math.atan2( A.r12, A.r13 ); //Roll
System.out.println("Gimbal lock: pitch = 90");
}
//General solution
else{
angle[0] = Math.atan2( A.r21, A.r11 );
angle[2] = Math.atan2( A.r32, A.r33 );
System.out.println("No gimbal lock");
}
return angle; //Euler angles in order yaw, pitch, roll
}
Rotating Points using a Rotation Matrix:
Given rotation matrix R, an arbitrary point can be rotated using the equation:
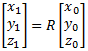
(eq 5)
In algebraic form, this expands to:
where:
The Java implementation of Equations 6a through 6c is shown in Code Sample 4. The input argument p_in is a three-element array of type double that contains the x, y and z values of the point to be rotated. On return, the contents of p_in will not have changed. The returned value is a new three-element array of type double that contains the x, y and z values of the rotated point.
Code Sample 4: Rotating a Point using a Rotation Matrix
public static double[] rotatePoint(
RotationMatrix A,
double[] p_in ) //Input coords in order (x,y,z)
{
double[] p_out = new double[3];
p_out[0] = A.r11*p_in[0] + A.r12*p_in[1] + A.r13*p_in[2];
p_out[1] = A.r21*p_in[0] + A.r22*p_in[1] + A.r23*p_in[2];
p_out[2] = A.r31*p_in[0] + A.r32*p_in[1] + A.r33*p_in[2];
return p_out; //Output coords in order (x,y,z)
}
Inverse Rotations
For rotation matrices, the transpose of a matrix equals its inverse. Therefore if Rf is a forward rotation matrix, the reverse rotation Rr can be obtained by transposing the rows and columns of Rf.
| Forward rotation matrix: |  |
(eq 7a) |
|
| Reverse rotation matrix: |  |
(eq 7b) |
Code Sample 5: Inverting a 3x3 Rotation Matrix
public static RotationMatrix transposeMatrix( RotationMatrix A )
{
RotationMatrix B = new RotationMatrix();
B.r11 = A.r11;
B.r12 = A.r21;
B.r13 = A.r31;
B.r21 = A.r12;
B.r22 = A.r22;
B.r23 = A.r32;
B.r31 = A.r13;
B.r32 = A.r23;
B.r33 = A.r33;
return B;
}
Combining Multiple Rotations
Multiple rotations can be combined into a single rotation by multiplying the respective rotation matrices together. If A is an initial rotation, and B is a subsequent rotation, then the cumulative rotation C is:

(eq 8)
where:
Code Sample 6 performs the 3x3 matrix multiplication described in equation 8. The function returns a new 3x3 rotation matrix.
Code Sample 6: Concatenating Rotations using Matrix Multiplication
public static RotationMatrix multiplyMatrices(
RotationMatrix A, //First rotation
RotationMatrix B ) //Second rotation
{
RotationMatrix C = new RotationMatrix();
C.r11 = A.r11*B.r11 + A.r12*B.r21 + A.r13*B.r31;
C.r12 = A.r11*B.r12 + A.r12*B.r22 + A.r13*B.r32;
C.r13 = A.r11*B.r13 + A.r12*B.r23 + A.r13*B.r33;
C.r21 = A.r21*B.r11 + A.r22*B.r21 + A.r23*B.r31;
C.r22 = A.r21*B.r12 + A.r22*B.r22 + A.r23*B.r32;
C.r23 = A.r21*B.r13 + A.r22*B.r23 + A.r23*B.r33;
C.r31 = A.r31*B.r11 + A.r32*B.r21 + A.r33*B.r31;
C.r32 = A.r31*B.r12 + A.r32*B.r22 + A.r33*B.r32;
C.r33 = A.r31*B.r13 + A.r32*B.r23 + A.r33*B.r33;
return C; //Returns combined rotation (C=AB)
}
}
Comments and error reports may be sent to the following address. We may post comments of general interest. Be sure to identify the page you are commenting on.
 .
.