Rotating Points in Two-Dimensions
D. Rose - December, 2014
Abstract
This tutorial describes the efficient way to rotate points around an arbitrary center on a two-dimensional (2D) Cartesian plane. This is a very common operation used in everything from video games to image processing. Sample code is provided in Java.
The Naïve Solution (don’t do this)
Let’s try a concrete example. Take the point (4,3) and rotate it 30 degrees around the origin in a counterclockwise direction. If you’ve taken high school trigonometry, you might come up with a solution like this:
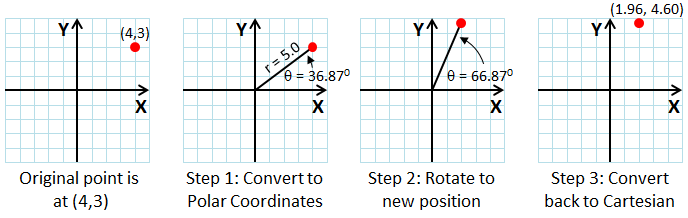
| Step 1: |
Convert the point from Cartesian to polar coordinates. Polar coordinates define the location of a point by its distance from the origin (r) and angle from the x-axis (θ).
|
|
| Step 2: | Rotate the point by 30°. You do this by adding 36.87°+30°, to get a rotated angle of 66.87°. | |
| Step 3: |
Convert back to Cartesian coordinates.
|
The Right Way
Equations 1 and 2 show the right way to rotate a point around the origin:
If we plug in our example point of (x0, y0) = (4, 3) and θ = 30°, we get the answer (x1, y1) = (1.964, 4.598), the same as before.
At first glance this may not seem to be that much faster than the naïve method, since it takes four trig functions, four multiplications, and two additions. The trick is that the trig functions only have to operate on the rotation angle, which is constant for all points. You therefore only have to compute them once, no matter how many points you are rotating. The per-point computational load is therefore only four multiplies and two additions—less than half that of the naïve method.
Rotating Points around an Arbitrary Center
But what if we want to rotate our point around something other than the origin? We simply modify equation 1 and 2 as follows:
where:
| (x0, y0) | = Point to be rotated | |
| (xc, yc) | = Coordinates of center of rotation | |
| θ | = Angle of rotation (positive counterclockwise) | |
| (x1, y1) | = Coordinates of point after rotation |
Note that if (xc, yc) = (0, 0), then equations 3 and 4 simplify to become equations 1 and 2, which is what we expect.
Sample Code:
This listing shows a Java implementation of equations 3 and 4. Note that the sine and cosine calculations are performed only once, outside the main loop. This saves significant computation time.
void rotatePoints(
double[] x, //X coords to rotate - replaced on return
double[] y, //Y coords to rotate - replaced on return
double cx, //X coordinate of center of rotation
double cy, //Y coordinate of center of rotation
double angle) //Angle of rotation (radians, counterclockwise)
{
double cos = Math.cos(angle);
double sin = Math.sin(angle);
double temp;
for( int n=0; n<x.length; n++ ){
temp = ((x[n]-cx)*cos - (y[n]-cy)*sin) + cx;
y[n] = ((x[n]-cx)*sin + (y[n]-cy)*cos) + cy;
x[n] = temp;
}
return;
}
Here is an example of how the rotatePoints() method would be called:
double[] x = {0, 0, 0, 0, 0, 10, 20, 10}; //Create some test data
double[] y = {0, 10, 20, 30, 40, 40, 30, 20}; //Create some test data
double cx = 20; //X-coord of center of rotation
double cy = 30; //Y-coord of center of rotation
double angle = 45 * Math.PI/180; //convert 45 degrees to radians
//Rotate the points
rotatePoints( x, y, cx, cy, angle );
//Display the results
for( int n=0; n<x.length; n++ ){
System.out.println( ""+x[n]+","+y[n] );
}
The following figure shows the eight points from the example code before and after the rotation:
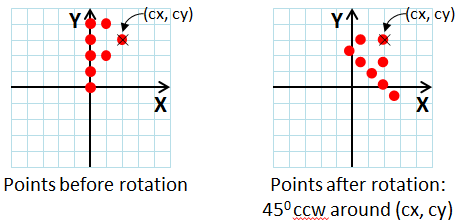
Common Errors
Here are a few things to be conscious of when implementing this code :- This function is designed to perform the rotation “in-place.” That is, the coordinate data in the x[] and y[] input arrays is replaced by their rotated equivalents when the rotatePoints() method returns. If you want to save the original points, you need to copy them first, or modify the method to write the results to separate arrays.
- Programming languages expect angles in radians. Neglecting to convert from degrees to radians is a common error.
- These examples assume a coordinate system where x points to the right and y points up. Unfortunately, most computer graphics systems use a convention where x points to the right and y points down. This has the effect of reversing the direction of rotation. If you use these equations in a y-down coordinate system, then a positive rotation angle will produce a clockwise rotation, rather than counterclockwise. You can correct for this by negating the sign of the rotation angle.
Comments and error reports may be sent to the following address. We may post comments of general interest. Be sure to identify the page you are commenting on.
 .
.