Solving 2x2, 3x3, 4x4 and 5x5 Systems of Linear Equations on a Computer

D. Rose - April, 2015

Abstract

One of the most common problems in linear algebra is the solving of simultaneous linear equations. There are several techniques available for accomplishing this, including Cramer's Method, Matrix Inversion, and Gaussian Elimination. Of these, Cramer's method is among the most efficient, and lends itself to the simplest software implementation. This paper describes an implementation of Cramer's method, and provides sample code in Java.

Solving a 2x2 System of Linear Equations:

A 2x2 system of linear equations has the following form. We assume the a_nn and k_n values are known, and the objective is to find the values of x₁ and x₂ that make both equations true:

(1a)

(1b)

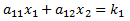
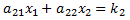
Using Cramer's Method, the solution is:

(2)

Where the determinant of a 2x2 matrix is:

(3)

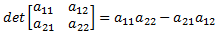
The full solution to a 2x2 system of linear equations can therefore be written as:

(4)

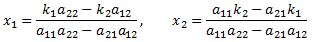
Note that the solution for both x₁ and x₂ have the same denominator. If the denominator is zero, then the system of equations has no unique solution. This will occur if the two lines described by equations 1a and 1b are parallel (in which case there are no solutions), or are the same line (in which case there are an infinite number of solutions). A computer implementation should check for this condition to prevent a divide-by-zero error.

Example Code for 2x2 Problem

Code Sample 1a shows a Java function that solves a 2x2 system of linear equations. Two functions are required:

solve2x2LinearEquation(): This function calculates the solution to a 2x2 system of linear equations. It takes six input arguments, which are the coefficients of the two linear equations as defined in Equation 1. It returns an array of type double that contains the values of x₁ and x₂. If there is no unique solution, the function returns null.
findDet2x2(): This is a private helper function that is called by solve2x2LinearEquation(). It calculates the determinant of a 2x2 matrix.

Code Sample 1a: Solution to 2x2 System of Linear Equations


public class LinearEquations
{
    public static double[] solve2x2LinearEquation(
            double a11, double a12, 
            double a21, double a22,
            double k1,  double k2 )
    {
        double det = findDet2x2( a11, a12, a21, a22 );
        if( det == 0.0 )
        {
            return( null );    //No unique solution
        }
        double[] result = { (k1*a22 - k2*a12) / det, (k2*a11 - k1*a21) / det };
        return( result );
    }

    private static double findDet2x2( double a11, double a12, double a21, double a22 ){
        return( a11*a22 - a21*a12 );
    }

    /* Subsequent methods go here  */
}

Code Sample 1b shows how this method would be used to solve the following equation. The solution is (x₁, x₂) = (−2, −4).

2x₁ + 3x₂ = −16

5x₁ − 10x₂ = 30

Code Sample 1b: Calling solve2x2LinearEquation()


public static void main(String[] args) {

    double[] answer = LinearEquations.solve2x2LinearEquation( 2, 3, 5, -10, -16, 30 );

    if( answer == null ){
        System.out.println( "No unique solution exists" );
    }
    else
    {
        System.out.println( "x1 = "  + answer[0] );	//x1 = -2
        System.out.println( "x2 = "  + answer[1] );	//x2 = -4
    }
}

Solving a 3x3 System of Linear Equations:

A 3x3 system of linear equations has the following form. We assume the a_nn and k_n values are known, and the objective is to find the values of x₁, x₂ and x₃ that make all three equations true:

(5a)

(5b)

(5c)

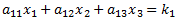
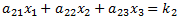
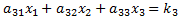
Using Cramer's Method, the solution is:

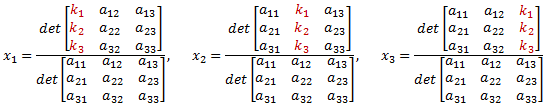
(6)

Where the determinant of a 3x3 matrix is:

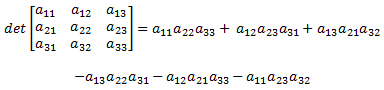
(7)

The full solution to a 3x3 system of linear equations can therefore be written as:

(8a)

(8b)

(8c)

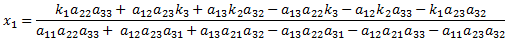
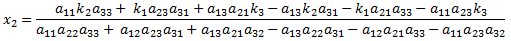
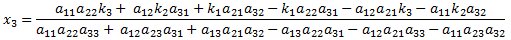
Note that the solution for x₁, x₂ and x₃ all have the same denominator. If the denominator is zero, then the system of equations has no unique solution. This will occur if at least two of the three planes described by equation 5 are parallel (in which case there are no solutions), or are the same plane (in which case there are an infinite number of solutions). A computer implementation should check for this condition to prevent a divide-by-zero error.

Example Code for 3x3 Problem

Code Sample 2a shows a Java function that solves a 3x3 system of linear equations. Two functions are required:

solve3x3LinearEquation(): This function calculates the solution to a 3x3 system of linear equations. It takes twelve input arguments, which are the coefficients of the three linear equations as defined in Equation 5. It returns an array of type double that contains the values of x₁, x₂ and x₃. If there is no unique solution, the function returns null.
findDet3x3(): This is a private helper function that is called by solve3x3LinearEquation(). It calculates the determinant of a 3x3 matrix.

Code Sample 2a: Solution to 3x3 System of Linear Equations


public class LinearEquations
{
    /* Prior methods go here  */

    public static double[] solve3x3LinearEquation( 
            double a11, double a12, double a13, 
            double a21, double a22, double a23,
            double a31, double a32, double a33,
            double k1,  double k2,  double k3 )
    {
        double det = findDet3x3( a11, a12, a13, a21, a22, a23, a31, a32, a33 );
        if( det == 0.0 )
        {
            return( null );    //No unique solution
        }

        double[] answer = new double[3];
        answer[0] = findDet3x3( k1,  a12, a13,  k2, a22, a23,  k3, a32, a33 )/det;
        answer[1] = findDet3x3( a11,  k1, a13, a21,  k2, a23, a31,  k3, a33 )/det;
        answer[2] = findDet3x3( a11, a12,  k1, a21, a22,  k2, a31, a32,  k3 )/det;
        return( answer );
    }
        
    private static double findDet3x3( 
            double a11, double a12, double a13, 
            double a21, double a22, double a23,
            double a31, double a32, double a33 )
    {
        return( a11*a22*a33 + a12*a23*a31 + a13*a21*a32 -
                a13*a22*a31 - a12*a21*a33 - a11*a23*a32 );
    }
    
    /* Subsequent methods go here  */
}

Code Sample 2b shows how this method would be used to solve the following equation. The solution is (x₁, x₂, x₃) = (−2, 3, 1).

−3x₁ + 2x₂ − 6x₃ = 6

5x₁ + 7x₂ − 5x₃ = 6

1x₁ + 4x₂ − 2x₃ = 8

Code Sample 2b: Calling solve3x3LinearEquation()


public static void main(String[] args) {

    double[] answer = LinearEquations.solve3x3LinearEquation(
           -3, 2, -6, 5, 7, -5, 1, 4, -2, 6, 6, 8 );

    if( answer == null ){
        System.out.println( "No unique solution exists" );
    }
    else
    {
        System.out.println( "x1 = "  + answer[0] );  //x1 = -2
        System.out.println( "x2 = "  + answer[1] );  //x2 =  3
        System.out.println( "x3 = "  + answer[2] );  //x3 =  1
    }
}

Solving a 4x4 System of Linear Equations:

A 4x4 system of linear equations has the following form. We assume the a_nn and k_n values are known, and the objective is to find the values of x₁, x₂, x₃ and x₄ that make all four equations true:

(9a)

(9b)

(9c)

(9d)

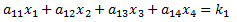
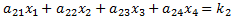
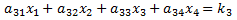
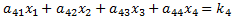
Using Cramer's Method, the solution is:

(10a, b)

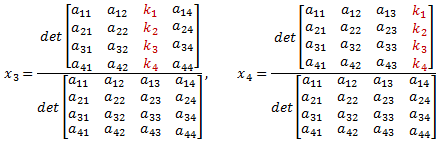
(10c, d)

The determinant of a 4x4 matrix is shown in equation 11. The determinants of the 3x3 submatrices in equation 11 can be calculated using equation 7.

(11)

Note that the solution for x₁, x₂, x₃ and x₄ all have the same denominator. If the denominator is zero, then the system of equations has no unique solution. This will occur if at least two of the four hyperplanes described by equation 9 are parallel (in which case there are no solutions), or are the same plane (in which case there are an infinite number of solutions). A computer implementation should check for this condition to prevent a divide-by-zero error.

Example Code for 4x4 Problem

Code Sample 3a shows a Java function that solves a 4x4 system of linear equations. Two functions are required:

solve4x4LinearEquation(): This function calculates the solution to a 4x4 system of linear equations. It takes 20 input arguments, which are the coefficients of the four linear equations as defined in Equation 9. It returns an array of type double that contains the values of x₁, x₂, x₃ and x₄. If there is no unique solution, the function returns null.
findDet4x4(): This is a private helper function that is called by solve4x4LinearEquation(). It calculates the determinant of a 4x4 matrix.

Code Sample 3a: Solution to 4x4 System of Linear Equations


public class LinearEquations
{
    /* Prior methods go here  */

    public static double[] solve4x4LinearEquation( 
            double a11, double a12, double a13, double a14, 
            double a21, double a22, double a23, double a24,
            double a31, double a32, double a33, double a34,
            double a41, double a42, double a43, double a44,
            double k1,  double k2,  double k3,  double k4 )
    {
        double det = findDet4x4( a11, a12, a13, a14, a21, a22, a23, a24,
                                 a31, a32, a33, a34, a41, a42, a43, a44 );
        
        if( det == 0.0 )
        {
            return( null );    //No unique solution
        }

        double[] answer = new double[4];
        answer[0] = findDet4x4(  k1, a12, a13, a14, k2,  a22, a23, a24,
                                 k3, a32, a33, a34, k4,  a42, a43, a44 )/det;
        answer[1] = findDet4x4( a11,  k1, a13, a14, a21,  k2, a23, a24,
                                a31,  k3, a33, a34, a41,  k4, a43, a44 )/det;
        answer[2] = findDet4x4( a11, a12,  k1, a14, a21, a22,  k2, a24,
                                a31, a32,  k3, a34, a41, a42,  k4, a44 )/det;
        answer[3] = findDet4x4( a11, a12, a13,  k1, a21, a22, a23,  k2,
                                a31, a32, a33,  k3, a41, a42, a43,  k4 )/det;
        return( answer );
    }    
    
    private static double findDet4x4( 
            double a11, double a12, double a13, double a14, 
            double a21, double a22, double a23, double a24,
            double a31, double a32, double a33, double a34,
            double a41, double a42, double a43, double a44 )
    {
        return( a11*findDet3x3(a22, a23, a24, a32, a33, a34, a42, a43, a44) -
                a12*findDet3x3(a21, a23, a24, a31, a33, a34, a41, a43, a44) +
                a13*findDet3x3(a21, a22, a24, a31, a32, a34, a41, a42, a44) -
                a14*findDet3x3(a21, a22, a23, a31, a32, a33, a41, a42, a43));
    }
        
    /* Subsequent methods go here  */
}

Code Sample 3b shows how this method would be used to solve the following equation. The solution is (x₁, x₂, x₃, x₄) = (−1, 1, −2, 3).

4x₁ + 1x₂ + 2x₃ − 3x₄ = −16

−3x₁ + 3x₂ − 1x₃ + 4x₄ = 20

−1x₁ + 2x₂ + 5x₃ + 1x₄ = −4

5x₁ + 4x₂ + 3x₃ − 1x₄ = −10

Code Sample 3b: Calling solve4x4LinearEquation()


public static void main(String[] args) {

    double[] answer = LinearEquations.solve4x4LinearEquation(
            4,  1,  2,  -3,
           -3,  3, -1,   4,
           -1,  2,  5,   1,
            5,  4,  3,  -1,
          -16, 20, -4, -10);

    if( answer == null ){
        System.out.println( "No unique solution exists" );
    }
    else
    {
        System.out.println( "x1 = "  + answer[0] );  //x1 = -1
        System.out.println( "x2 = "  + answer[1] );  //x2 =  1
        System.out.println( "x3 = "  + answer[2] );  //x3 = -2
        System.out.println( "x4 = "  + answer[3] );  //x4 =  3
    }
}

Solving a 5x5 System of Linear Equations:

A 5x5 system of linear equations has the following form. We assume the a_nn and k_n values are known, and the objective is to find the values of x₁, x₂, x₃, x₄ and x₅ that make all five equations true:

(12a)

(12b)

(12c)

(12d)

(12e)

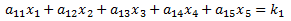
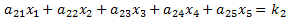
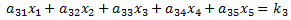
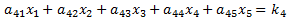
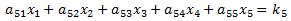
Using Cramer's Method, the solution is:

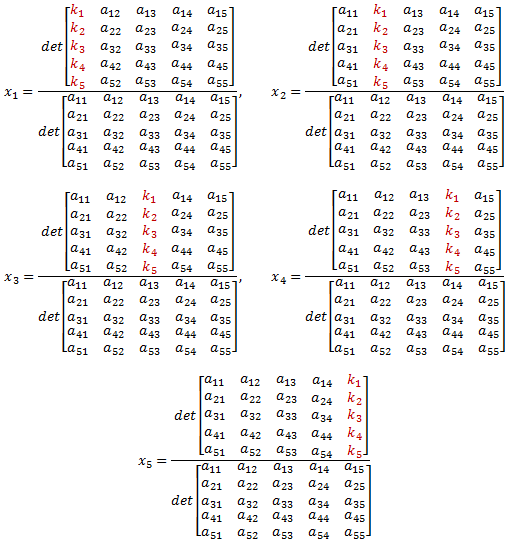
(13)

The determinant of a 5x5 matrix is shown in equation 14. The determinants of the 4x4 submatrices in equation 14 can be calculated using equation 11.

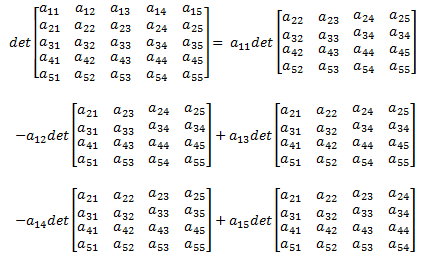
(14)

Note that the solution for x₁, x₂, x₃, x₄ and x₅ all have the same denominator. If the denominator is zero, then the system of equations has no unique solution. This will occur if at least two of the four hyperplanes described by equation 12 are parallel (in which case there are no solutions), or are the same plane (in which case there are an infinite number of solutions). A computer implementation should check for this condition to prevent a divide-by-zero error.

Example Code for 5x5 Problem

Code Sample 4a shows a Java function that solves a 5x5 system of linear equations. Two functions are required:

solve5x5LinearEquation(): This function calculates the solution to a 5x5 system of linear equations. It takes 30 input arguments, which are the coefficients of the five linear equations as defined in Equation 12. It returns an array of type double that contains the values of x₁, x₂, x₃, x₄ and x₅. If there is no unique solution, the function returns null.
findDet5x5(): This is a private helper function that is called by solve5x5LinearEquation(). It calculates the determinant of a 5x5 matrix.

Code Sample 4a: Solution to 5x5 System of Linear Equations


public class LinearEquations
{
    /* Prior methods go here  */

    public static double[] solve5x5LinearEquation( 
            double a11, double a12, double a13, double a14, double a15, 
            double a21, double a22, double a23, double a24, double a25,
            double a31, double a32, double a33, double a34, double a35,
            double a41, double a42, double a43, double a44, double a45,
            double a51, double a52, double a53, double a54, double a55,
            double k1,  double k2,  double k3,  double k4,  double k5 )
    {
        double det = findDet5x5( a11, a12, a13, a14, a15, a21, a22, a23, a24, a25,
                                 a31, a32, a33, a34, a35, a41, a42, a43, a44, a45,
                                 a51, a52, a53, a54, a55 );
        
        if( det == 0.0 )
        {
            return( null );    //No unique solution
        }

        double[] answer = new double[5];
        answer[0] = findDet5x5(   k1, a12, a13, a14, a15,  k2, a22, a23, a24, a25,
                                  k3, a32, a33, a34, a35,  k4, a42, a43, a44, a45,
                                  k5, a52, a53, a54, a55)/det;
        answer[1] = findDet5x5(  a11,  k1, a13, a14, a15, a21,  k2, a23, a24, a25,
                                 a31,  k3, a33, a34, a35, a41,  k4, a43, a44, a45,
                                 a51,  k5, a53, a54, a55)/det;
        answer[2] = findDet5x5(  a11, a12,  k1, a14, a15, a21, a22,  k2, a24, a25,
                                 a31, a32,  k3, a34, a35, a41, a42,  k4, a44, a45,
                                 a51, a52,  k5, a54, a55)/det;
        answer[3] = findDet5x5(  a11, a12, a13, k1, a15, a21,  a22, a23,  k2, a25,
                                 a31, a32, a33, k3, a35, a41,  a42, a43,  k4, a45,
                                 a51, a52, a53, k5, a55)/det;
        answer[4] = findDet5x5(  a11, a12, a13, a14,  k1, a21, a22, a23, a24,  k2,
                                 a31, a32, a33, a34,  k3, a41, a42, a43, a44,  k4,
                                 a51, a52, a53, a54,  k5)/det;
        return( answer );
    }
	
    private static double findDet5x5(
            double a11, double a12, double a13, double a14, double a15, 
            double a21, double a22, double a23, double a24, double a25,
            double a31, double a32, double a33, double a34, double a35,
            double a41, double a42, double a43, double a44, double a45,
            double a51, double a52, double a53, double a54, double a55 )
    {
        return( a11*findDet4x4(a22, a23, a24, a25, a32, a33, a34, a35, a42, a43, a44, a45, a52, a53, a54, a55 ) -
                a12*findDet4x4(a21, a23, a24, a25, a31, a33, a34, a35, a41, a43, a44, a45, a51, a53, a54, a55 ) +
                a13*findDet4x4(a21, a22, a24, a25, a31, a32, a34, a35, a41, a42, a44, a45, a51, a52, a54, a55 ) -
                a14*findDet4x4(a21, a22, a23, a25, a31, a32, a33, a35, a41, a42, a43, a45, a51, a52, a53, a55 ) +
                a15*findDet4x4(a21, a22, a23, a24, a31, a32, a33, a34, a41, a42, a43, a44, a51, a52, a53, a54 ));
    }	
}

Code Sample 4b shows how this method would be used to solve the following equation. The solution is (x₁, x₂, x₃, x₄, x₅) = (−15.354, 15.813, −1.770, −22.148, −6.660).

4x₁ + 1x₂ + 2x₃ − 3x₄ + 5x₅ = −16

−3x₁ + 3x₂ − 1x₃ + 4x₄ − 2x₅ = 20

−1x₁ + 2x₂ + 5x₃ + 1x₄ + 3x₅ = −4

5x₁ + 4x₂ + 3x₃ − 1x₄ + 2x₅ = −10

1x₁ − 2x₂ + 3x₃ − 4x₄ + 5x₅ = 3

Code Sample 4b: Calling solve5x5LinearEquation()


public static void main(String[] args) {

    double[] answer = LinearEquations.solve5x5LinearEquation(
            4,  1,  2,  -3,  5,
           -3,  3, -1,   4, -2,
           -1,  2,  5,   1,  3,
            5,  4,  3,  -1,  2,
            1, -2,  3,  -4,  5,
          -16, 20, -4, -10,  3);

    if( answer == null ){
        System.out.println( "No unique solution exists" );
    }
    else
    {
        System.out.println( "x1 = "  + answer[0] );  //x1 = -15.354
        System.out.println( "x2 = "  + answer[1] );  //x2 =  15.813
        System.out.println( "x3 = "  + answer[2] );  //x3 =  -1.770
        System.out.println( "x4 = "  + answer[3] );  //x4 = -22.148
        System.out.println( "x5 = "  + answer[4] );  //x5 =  -6.660
    }
}

Calling functions with 20 or 30 input arguments is a little tedious, and can be prone to coding errors. We have designed our function this way for simplicity and clarity. However, if your application already has a way of representing matrices (either one- or two-dimensional arrays, or a dedicated matrix class), it may be advisable to redesign these functions or put a wrapper around them so that they accept the more concise input representation.

Why Cramer's Method?

There are several methods for solving systems of linear equations. Why did we choose Cramer's Method? Here is an analysis of the two main competing techiques: Gaussian Elimination, and Matrix Inversion.

Comparison with Gaussian Elimination

If you search the Internet for techniques to solve simultaneous linear equations, you will find that most authors use the Gaussian Elimination method. Why? It turns out that Gaussian Elimination is a good technique if you are solving problems by hand. But it's not very convenient for computer programs.

Suppose we have a system of three linear equations:

(15a)

(15b)

(15c)

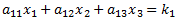
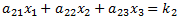
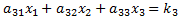
To solve this system using Gaussian Elimination, we need find a constant that we can multiply across one of the equations so that, when we add or subtract two equations from each other, one of the variables cancels out. For example, we could multiply equation 15a by (a₂₁/a₁₁) to get:

(16)

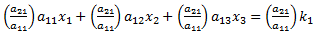
Which simplifies to:

(17)

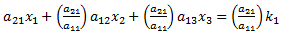
The coefficient of x₁ is now a₂₁, which is that same as the coefficient of x₁ in equation 15b. If we subtract (15b) from (17), the x₁ terms cancel, and we are left with only two unknowns. We can repeat this process using some other combination of rows to produce a second equation with only two unknowns, at which point we can easily solve the problem.

But what happens if a₁₁ happens to be zero? A computer implementation of this technique will produce a divide-by-zero error in the first step. Or what happens if a₂₁ is zero? In that case, equation 17 will reduce to 0=0, which is useless for solving the problem.

If we were solving the problem by hand, having some zero-valued coefficients actually speeds the process up, since it reduces the number of variables we need to eliminate. But that requires a judicious choice of which equations to use and which variables to eliminate. That's easy for a human. But a computer implementation must test for zero at all stages, resulting in a messy set of if-else statements. Many a programmer has coded up a Gaussian Elimination-type equation solver and successfully tested it on a handful of examples, only to have it fail intermittently when deployed. It can be made to work, but coding is tricky, and the result is less computationally efficient than Cramer's method.

Comparison with Matrix Inversion

Suppose we have a system of three linear equations:

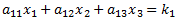
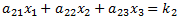
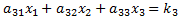
To solve this system using matrix inversion, we write the problem in matrix form.

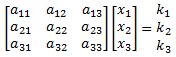
If [A] represents the 3x3 coefficient matrix, then:

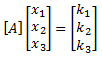
To solve this, we simply multiply both sides of the equation by [A^-1] and simplify to get:

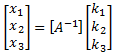
This equation says that to find (x₁, x₂, x₃), we need to find the inverse of the 3x3 matrix A, and multiply it by the 1x3 matrix K.

The inverse of a 3x3 matrix is another 3x3 matrix, which can be found as follows:

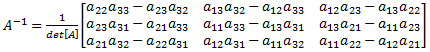
where:

If the determinant is not zero, the solution can be computed directly as follows.

(eq 18a)

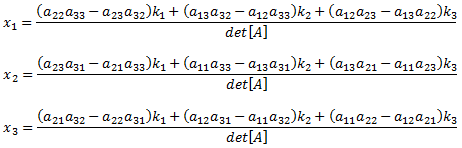
(eq 18b)

(eq 18c)

With minor algebraic manipulations, it can be shown that this is the same as the Cramer's Method solution in equation 8. A similar proof will hold true for any sized set of linear equations. The conclusion is that the two solutions are identical: Cramer's Method is just a convenient way of summarizing the matrix inversion solution.

Comments and error reports may be sent to the following address. We may post comments of general interest. Be sure to identify the page you are commenting on.

Email address as an image to prevent spamming .