Engineering Notes -- Home
A note from the author
As a practicing aerospace engineer, I frequently encounter problems that require math skills I don’t have and must learn. Early in my career I adopted the habit of writing down the solutions to these problems in a personal Engineering Notebook. If a problem took more than a trivial amount of time to research, and was general enough that I might run into it again some day, into the notebook it went.
The articles on this website are based on those engineering notes. They represent practical, battle-tested solutions to real-world problems. Technology changes, but math is eternal. I hope these papers save you some time.
| |
 |
|
Converting between Earth-Centered, Earth Fixed and Geodetic Coordinates
How to convert from Geodetic coordinates (latitude, longitude and height above ellipsoid) to Earth-Centered, Earth-Fixed coordinates, and back again. Includes example code. |
| |
 |
|
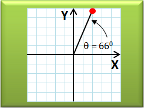
Rotating Points in Two-Dimensions
The efficient way to rotate points around an arbitrary center on a two-dimensional Cartesian plane. |
| |
 |
|
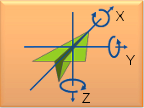
Rotations in Three-Dimensions: Euler Angles and Rotation Matrices
Describes a commonly used set of Tait-Bryan Euler angles, and shows how to convert from Euler angles to a rotation matrix and back. |
| |
 |
|
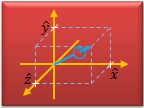
Rotation Quaternions, and How to Use Them
An introduction to rotation quaternions. Shows how to perform rotations, and how to convert between quaternions, rotation matrices, axis-angle, and Euler angles. |
| |
 |
|
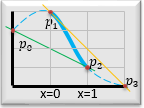
Solving 2x2, 3x3, 4x4 and 5x5 Systems of Linear Equations on a Computer
A general solution to systems of linear equations of up to 5 equations and 5 unknowns, using Cramer's Method. |
| |
 |
|
Interpolation
Methods for interpolating one-dimensional signals, images, and 2D graphics. Based on Catmull-Rom cubic spline. |
| |
 |
|
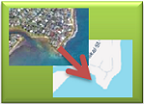
Rigid-Body Image Registration
A tiepoint-based error-minimization method for registering two images, where the degrees of freedom are limited to translation, rotation and scale. |
Comments and error reports may be sent to the following address. We may post comments of general interest. Be sure to identify the page you are commenting on.
 .
.
 .
.






